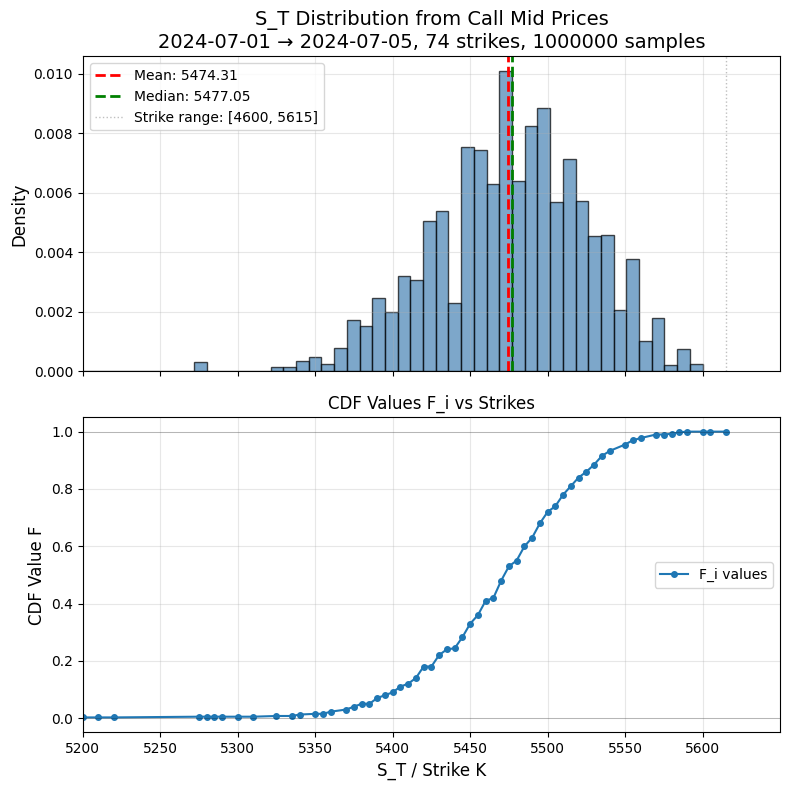
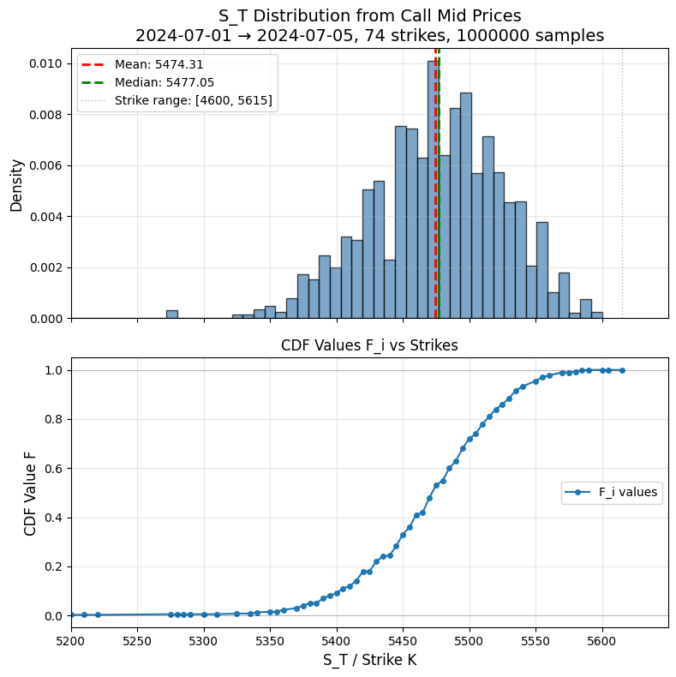
For a single maturity, European call prices encode the risk-neutral distribution of the underlying. You can turn them into Monte Carlo samples without fitting a model or estimating a density.
For strikes ![]() with call prices
with call prices ![]() , define
, define
![]()
This is a discrete approximation of the cumulative distribution function of ![]() .
.
To sample:
- Draw
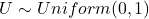
- Find
 such that
such that 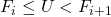
- Set
![]()
Repeat for as many samples as needed.
This produces risk-neutral samples directly from observed call prices using only simple finite differences. It’s fully model-free, requires no volatility surface fitting, and preserves arbitrage constraints!
Below and example results from S&P500 option prices: