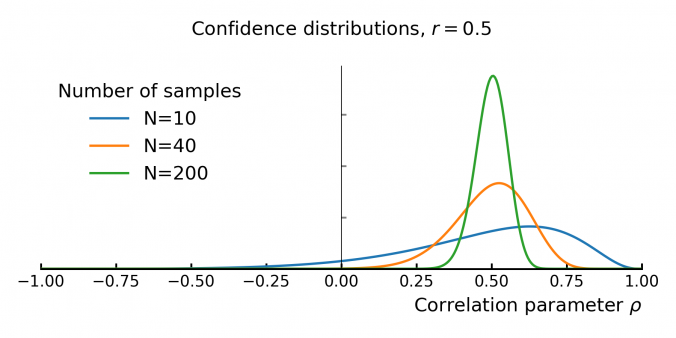
Correlation is everywhere in finance. It’s the backbone of portfolio optimization, risk management, and models like the CAPM. The idea is simple: mix assets that don’t move in sync, and you can reduce risk without sacrificing too much return. But there’s a problem—correlation is usually taken at face value, even though it’s often some form of an estimate based on historical data. …and that estimate comes with uncertainty!
This matters because small errors in correlation can throw off portfolio models. If you overestimate diversification, your portfolio might be riskier than expected. If you underestimate it, you could miss out on returns. In models like the CAPM, where correlation helps determine expected returns, bad estimates can lead to bad decisions.
Despite this, some asset managers don’t give much thought to how unstable correlation estimates can be. In this post, we’ll dig into the uncertainty behind empirical correlation, and how to quantify it.
Continue reading