Category: DevOps/MLOps/Code

New open-source library: Conditional Gaussian Mixture Models (CGMM)

August 31, 2025 / Thijs van den Berg

pip install cgmm

I’ve released a small, lightweight Python library that learns conditional distributions and turns them e.g. into scenarios, fan charts, and risk bands with just a few lines of code. It’s built on top of scikit-learn (fits naturally into sklearn-style workflows and tooling).

Example usage:

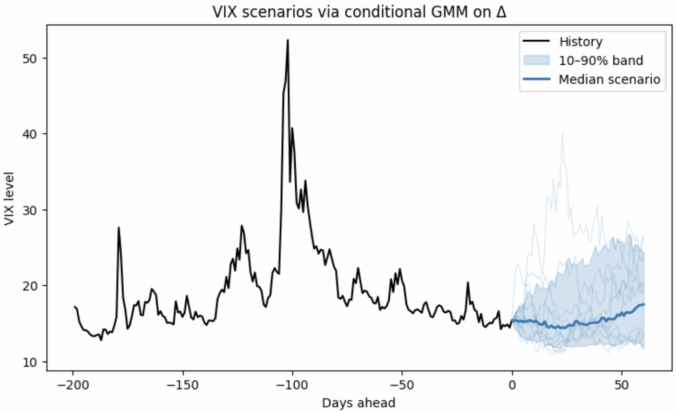
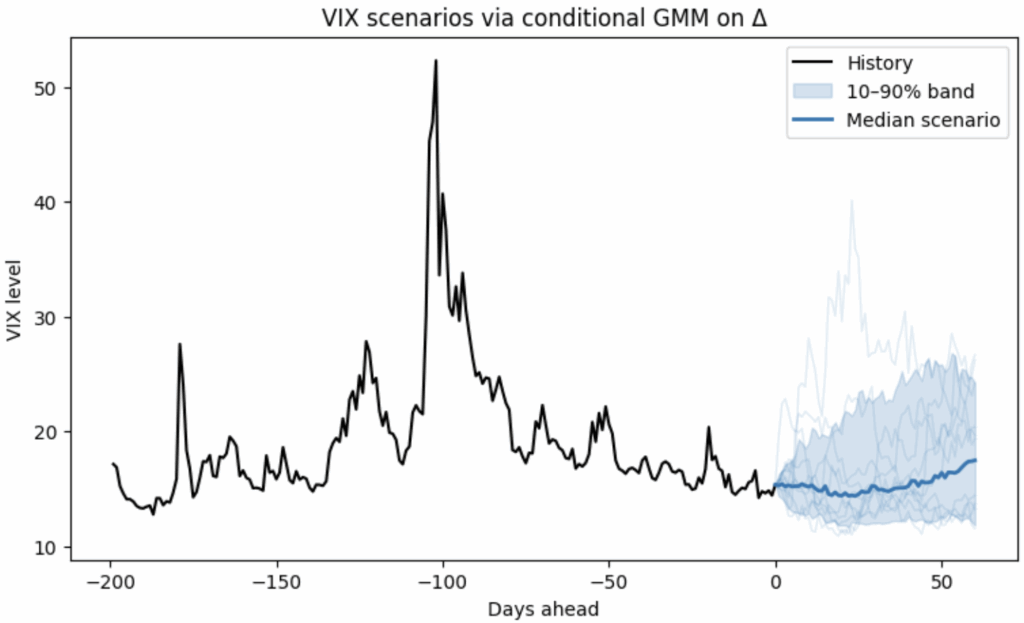
In the figure below, a non-parametric model is fit on ΔVIX conditioned on the VIX level, so it naturally handles:

Non-Gaussian changes (fat tails / asymmetry), and
Non-linear, level-dependent drift (behavior differs when VIX is low vs. high).

Features:

Conditional densities and scenario generation for time series and tabular problems
Quantiles, prediction intervals, and median/mean paths vuia MC simulation
Multiple conditioning features (macro, technicals, regimes, etc.)
Lightweight & sklearn-friendly; open-source and free to use (BSD-3)

VIX example notebook: https://cgmm.readthedocs.io/en/latest/examples/vix_predictor.html

Call for examples & contributions:

Do you have a use-case we should showcase (rates, spreads, realized vol, token flows, energy, demand, order-book features…)?
Send a brief description or PR—examples will be attributed.
Contributions, issues, and feature requests are very welcome. And if you find this useful, please share or star the repo to help others discover it.

Not investment advice. The library is still work in progress!

Parallel Processing of Tasks with Python’s Multiprocessing lib

December 29, 2020 / Thijs van den Berg

The Python code snippet below uses the multiprocessing library to processes a list of tasks in parallel using a pool of 5 threads.

note: Python also has a multithreading library called “threading”, but it is well documented that Python multithreading doesn’t work for CPU-bound tasks due to Python’s Global Interpreter Lock (GIL), for more info google: “python multithreading gil”.

from multiprocessing import Process, Pool

import itertools
import time


def train(opt, delay=2.0):
    time.sleep(delay)
    return f'Done training {opt}'


# Grid search
grid = {
    'batch_size': [32, 64, 128],
    'learning_rate': [1E-4, 1E-3, 1E-2]
}


def main():
    settings_list = []
    for values in itertools.product(*grid.values()):
        settings_list.append( dict(zip(grid.keys(), values)) )

    with Pool(5) as p:
        print(p.map(train, settings_list))


if __name__ == "__main__":
    main()

Output

[
"Done training {'batch_size': 32, 'learning_rate': 0.0001}", 
"Done training {'batch_size': 32, 'learning_rate': 0.001}", 
"Done training {'batch_size': 32, 'learning_rate': 0.01}", 
"Done training {'batch_size': 64, 'learning_rate': 0.0001}", 
"Done training {'batch_size': 64, 'learning_rate': 0.001}", 
"Done training {'batch_size': 64, 'learning_rate': 0.01}", 
"Done training {'batch_size': 128, 'learning_rate': 0.0001}", 
"Done training {'batch_size': 128, 'learning_rate': 0.001}", 
"Done training {'batch_size': 128, 'learning_rate': 0.01}"
]

Parameter Grid-searching with Python’s itertools

December 29, 2020 / Thijs van den Berg

Python’s Itertools offers a great solution when you want to do a grid-search for optimal hyperparameter values, -or in general generate sets of experiments-.

In the code fragment below we generate experiment settings (key-value pairs stored in dictionaries) for all combinations of batch sizes and learning rates.

import itertools

# General settings
base_settings = {'epochs': 10}

# Grid search
grid = {
    'batch_size': [32, 64, 128],
    'learning_rate': [1E-4, 1E-3, 1E-2]
}

# Loop over al grid search combinations
for values in itertools.product(*grid.values()):
    point = dict(zip(grid.keys(), values))

    # merge the general settings
    settings = {**base_settings, **point}

    print(settings)

output:

{'epochs': 10, 'batch_size': 32, 'learning_rate': 0.0001}
{'epochs': 10, 'batch_size': 32, 'learning_rate': 0.001}
{'epochs': 10, 'batch_size': 32, 'learning_rate': 0.01}
{'epochs': 10, 'batch_size': 64, 'learning_rate': 0.0001}
{'epochs': 10, 'batch_size': 64, 'learning_rate': 0.001}
{'epochs': 10, 'batch_size': 64, 'learning_rate': 0.01}
{'epochs': 10, 'batch_size': 128, 'learning_rate': 0.0001}
{'epochs': 10, 'batch_size': 128, 'learning_rate': 0.001}
{'epochs': 10, 'batch_size': 128, 'learning_rate': 0.01}